Vicclap fórum téma:Agyaló
Menü:
Bejelentkezés
Partnerek
Kategóriák
Fórum témáim
Vicclap fórum
2011. július 23 14:07:29
Lóláb
Egy lónak két lába 10 kilométert tesz meg egy nap alatt, másik két lába meg ugyanazon a napon 11-et. Hogyan lehetséges ez úgy, hogy közben a ló épségben marad?
Igen, bónusz pont a gyorsaságért és a pontosan egy peres válaszidőért.
Megoldás: körbe-köbe jár.
Megfejtő: esernyo
2011. július 23 13:54:08
Úristen mikről beszéltek már megint... Én tegnap óta sem lettem okosabb, maradok a szóláncnál, az még megy valahogy.
De azért olvaslak ám titeket továbbra is, annak ellenére, hogy nem értem, érdekesnek találom.
Neeem, egyáltalán nem, tényleg. Csak agyilag kevés vagyok a megértéséhez.
Persze a megoldásokat olvasva néha a falnak tudnék futni, hogy tényleg, de magamtól sose jönnék rá. Másban vagyok jó...
Engem nem zavar, még szórakoztat is ez az "adok-kapok", hiába nem értem. Végre megint van valami élet a fórumban.
2011. július 23 13:29:35
Egy sorozat (igaz nem számokból, hanem betűkből):
B, H, F, V, K, ?, ?, ?
Mi lehet a három hiányzó betű?
Így van, és a magyar szakkifejezés hű az eredetihez, ahol a szultán "nagyvezíre" áll a szultán mellett.
Val, mondanám, hogy kapsz egy fagyit, vagy megtanítalak szuper kis lufikardot hajtogatni (pont ma hallottam, hogy akár nemzetközileg elismert vizsgát is lehet tenni lufihajtogatásból), de maximum csak gondolatban menne ez most, innen a vízről.
Tehát a helyes megoldás: F, H, B, mint futó, huszár, bástya.
Helyes megfejtő: Val
már az elején feltűnt, hogy miért éppen 3 következő betűt kell kitalálni, és összesen nyolcan vannak... de az, hogy utána külön felhívtad erre a figyelmet, még inkább ebben az irányban keresgéltem, aztán leesett!
Egészen jó feladat, főleg hogy sokan a huszárt lónak, és a vezért királynőnek nevezik. A paraszt gyalogokról nem is beszélve...
2011. július 23 13:12:28
Borbély
Van egy faluban egy borbélyműhely. A borbély népszerűsíteni szeretné az üzletét, ezért kijelenti, hogy minden férfit megborotvál a faluban, aki nem borotválkozik. Mi a hiba ebben a kijelentésben?
(tegyük fel, hogy nem divat a nagy szakáll a faluban, tehát nem sértődik meg senki, hogy márpedig őt nem borotválja senki)
Hát de nyilván van olyan aki hol megborotválkozik, hol borbélyhoz megy... Azokkal mi a helyzet? :) És vajon a borbély nem jár át a szomszéd faluba egy másik borbélyhoz?
Az előítélet nem feltéltenül mindig rossz dolog. Ha tapasztalatból tudjuk, hogy például a borbélyok legalább 99%-a férfi, akkor egy ismeretlen nemű borbély esetén jogosan feltételezhetjök, hogy szintén férfi, míg meg nem győződünk az ellenkezőjéről.
Ha pedig nőnemű a borbély, akkor tényleg nincs gond a kijelentésével. Ez a feladvány más nyelven egyértelműbb lett volna, mert akkor lehetett volna feltűnés nélkül így fogalmazni: "er sagt", "he says", stb.
2011. július 23 12:37:21
Lámák
Egy állatkert-igazgató 9 lámát helyet el egy nagy négyzet alakú ketrecben, valahogy így:
Ezek a lámák igen lomhák, és folyamatosan az ábrán látható helyzetben állnak. Tudsz-e mindegyiknek saját ketrecet biztosítani úgy, hogy csupán 2 másik, négyzet alakú kerítést építesz?
2011. július 23 12:35:24
Adott egy tucat csirke, egy mázsa zab, és egy ló. Hogyan lehet, hogy csirketáplálásra előbb fogy el a mázsa zab?
Ja így viszont már nem jó... :( Tudjátok hogy hova kerülnek a vágóhídon levágott lovak? Takarmányba :(
Így van. A feladatban az szerepelt, hogy "csirketáplálásra előbb fogy el a mázsa zab", nem pedig "csirketáplálásra fogy el előbb a mázsa zab."
2011. július 23 12:04:34
Ketten mennek a malomba. Józsi egy zsák lisztet cipelt a hátán, András három ugyanekkora zsákot vitt, mégis Józsi cipelte a nagyobb terhet. Hogy lehet ez?
Csak azért mert több feltételezés is volt az összetett mondatodban, de mivel tényleg a Tiéd a helyes megfejtés, tehát:
Megfejtő: esernyő
Megfejtés: András zsákjai üresek voltak
2011. július 23 11:57:02
Na akkor egy könnyűt és gyorsat megint: Egy észak-déli irányba haladó óceánjárón egy matróz áll a korláthoz dőlve, és kelet felé nézve szemléli a tengert. A hajó másik oldalán ugyancsak a korlátnak támaszkodva nyugat felé néz egy matróz. Állandóan a megadott irányba nézve azt mondja a kelet felé néző matróz a másiknak:
- Hallod-e, mitől kormos az orrod?
Megszólal erre a másik:
- A te inged eleje is csupa korom!
Hogyan látták meg ezt egymáson, amikor az egyik mindig kelet felé, a másik mindig nyugat felé nézett?
Vagy csak nagyon unták magukat, és már nem tudtak mit kitalálni maguk szórakoztatására, így mondtak egymásnak mindenféle badarságot .
De ugye mégis csak az első a helyes megfejtés, nagyon jó vagy ezekben.
2011. július 23 11:40:26
Milyen sapka van a fejeden?
Három ember azon vitatkozik, hogy melyikük a legokosabb. Elmennek a bölcshöz, hogy ő döntse el a kérdést. A bölcs a következő feladatot adja nekik: „Van 5 sapkám, 3 fekete és 2 fehér. Be fogjátok csukni a szemeteket, és közben én mindegyikőtök fejére ráteszek egy sapkát, a másik két sapkát pedig eldugom. Utána kinyithatjátok a szemeteket, és aki először kitalálja, hogy milyen színű sapka van a fején, az a legokosabb.”
Ezután a három ember becsukta a szemét, a bölcs mindegyiknek a fejére tett egy fekete sapkát, a két fehéret pedig eldugta. Miután kinyitották a szemüket, kis idő múlva az egyikük megszólalt: „Rajtam fekete sapka van.”
Hogyan jött rá?
Így már jó.
Házibulin jó lehet kipróbálni, az idő előrehaladtával exponenciálisan nehezebbnek éreznék a feladatot. Egyébként nagy hallgatás lenne belőle szerintem és röhögcsélés.
de ez még nem teljes... szóval ha rajta fehér sapka lett volna a másik kettőn meg fekete, akkor a másik kettőből szólt volna valaki hogy rajta fekete van, mivel senki más nem szólt hogy 2 fehér sapkát lát
mert látta hogy a másik férfin is két fekete sapka volt. Mivel ha rajta lett volna fehér sapka, és a másikon is fehér sapka lett volna, akkor a harmadik megszólalt volna hogy rajta fekete sapka van, mert ki lett lőve mind a két fehér sapka.
2011. július 23 00:49:47
Remélem nem utáltok ki innen, hogy most előveszek egy régebbi, meg nem válaszolt feladatot, és megolom:
Feladat (esernyo):
Folytasd a sorozatot (2)
1; 2; 6; 30; 210; ....
pi/2
Bizonyítás:
Azt az f(n) függvény keressük, melyre
f(0) = 1,
f(1) = 2,
f(2) = 6,
f(3) = 30,
f(4) = 210
Legyen f(n) = delta(x-n) pi/2 + g(x) (1-delta(x-n))
ahol
g(x)=g(x-1)(2x-1)
g(0) = 1
és delta(x) a Dirac delta függvény. Jelen feladatunk esetében a sorozat 5. elemét keressük (0-tól számolva), tehát n=5.
Így teljesünek a feltételek x = 0..4-re, és f(5) = pi/2
Magyarázat:
a g(x) függvény valójában az, amire a feladat szerzője eredetileg gondolhatott: úgy alkotom meg a sorozat x-ik elemét, hogy az előző elemet megszorzom az x-ik páratlan számmal. Eredetileg 210*9 = 1890-re gondolhatott a szerző.
Az f(x) függvény leírásában az összeg első tagja biztosítja, hogy csak az n-edik elem legyen pi/2, míg a második tagja azt biztosítja, hogy csak az n-edik elem NE legyen a g(x) függvény által megadott érték.
A Dirac delta függvény pedig ez:
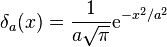ahol a --> 0. Keressetek rá a Wikipédián, a viselkedése sokkal
egyszerűbb és érthetőbb, mint amire a képlete alapján lehetne gondolni.Egy Dirac delta függvény nélküli változaton is gondolkoztam, kb. ehhez hasonló trükköket lehetne bevetni: ha azt akarom, hogy egy függvény mindig nulla legyen, míg kisebb, mint n, és pontosan n-re mondjuk pi/2 legyen az értéke, akkor ezt
(pi/2) (x (x-1) (x-2) (x-3) ... (x-n)) / n! biztosítja. Ehhez hasonló logikával lehet gondolkozni a második felének a megszerkesztésén is, ahol minden n-nél kisebbre kell 1 legyen az értéke, hogy ezt megszorozhassuk a "hivatalos" megoldással.
Előnye: nem kell a Dirac delta függvény, így középiskolában is érthető. Hátránya: n-nél nagyobb értékekre totális káosz lesz belőle, míg az első megoldás esetében szépen halad tovább a sorozat a "hivatalos" megoldás alapján, kivéve egyetlen egy pozícióban !!
Ezt az őrültséget bárki szabadon használhatja, csak az a kérésem, hogy ha valaki élesben beveti (pl. iskolában, versenyen), mondja el nekem milyen képet vágott hozzá a tanár.
Először az volt a baj, hogy direkt nem akartam belemenni disztribúcióelméleti kérdésekbe itt a fórumon, aztán meg az a baj, hogy belementem. \o/
Az alapkérdés az az, hogy mégis miért érezted úgy, hogy bármi köze van a Dirac deltának egy ilyen feladathoz. (függetlenül attól, hogy rosszul használtad, majd lecseszel hogy én a diszkrét Dirac deltáról beszélek te meg nem, majd pedig újra lecseszel, hogy te mégis a diszkrétről beszélsz, igaz úgy meg az általad megadott sorozat nem oda tart semmilyen értelemben...)A lényeg, hibát soha semmilyen körülmények közt ne ismerj be.
A megoldás pedig 2310, mivel a sorozat elején az előző elem 2, 3, 5 majd 7-szereződik, ezek meg nem sorban a páratlan számok, hanem a prímek.
Azt már említettem, hogy elírtam, és nem f(n), hanem f(x)-et akartam írni. Igen, talán azt is oda lehetett volna írni, hogy diszkrét térben vagyunk, de gondoltam egyértlemű, hiszen egy számsorozat diszkrét elemeiről beszélünk. Ha szakdolgozatot kellett volna írnom, nem pedig egy rövid szemléltetést, akkor az ilyesmikre jobban odafigyeltem volna.
Említsek olyan hivatkozásokat szakfolyóiratokban, ahol úgy használják a Dirac impulzust, mint ahogyan én használtam, vagy inkább ne folytassuk ezt a lassan túlzásba menő szőrszálhasogatást?
Csodálom milyen gyorsan fel tudod térképezni egy ember látókörét, egy fél oldal alapján. Ha valamit ebben a fél oldalban nem említettem, az ugyebár egyértelmű bizonyíték arra, hogy túl szűk a látóköröm ahhoz, hogy hallottam volna róla?
Valamiért levágta a felét, bocsi a fórummal még barátkoznom kell.
Ez badarság, a jobb oldal függ x-től, a bal oldal pedig nem. Gondolom arra gondoltál, hogy
Legyen f(x) = delta(x-5) pi/2 + g(x) (1-delta(x-5))
(a hiba nem egyszerű helyettesítsünk 5-öt az n helyébe, mert valahol x-re cserélődött az n)
De amúgy ez sem jó, mert a Dirac delta függvényt úgy szemléltethetjük, hogy mindenhol nulla, a nullában végtelen. Ha az általad újonnan említett diszkrét Dirac deltát vesszük, úgy már hellyel közzel jó. (ami amúgy a mértékelméletben rendelkezik olyan tulajdonságokkal, mint a Dirac delta, és abbéli tulajdonságait használják fel a jelfeldolgozásban, csak hogy tágítsam kicsit a látóköröd)
Az én példámat meg akkor módosíthatjuk úgy is, hogy az f függvény a 0-5 értékekre a már leírt, egyébként mindenhol máshol a 42 értéket veszi fel. Na, így jobb? Értelmezve van mindenhol...
Inkább csak a matematikai részre reagálok, a többi eléggé moderálásgyanús lenne. Erre is csak azért, mert olyan gonosz voltam, hogy téves bizonyítékokkal vádoltam...
"A Dirac delta meg valóban nevezhető függvénynek, és habár felírható diszkrét térben úgy, mint "mindenhol nulla, kivéve nullában, ahol 1", az általános meghatározása pontosan azzal a határátmenettel definiálódik, ez garantálja, hogy folytonos térben az integrálja egy. "
A diszkrét Dirac delta valóban az, hogy mindenhol 0 az értéke kivéve a nullában, ahol 1. Nem erre gondoltam. A Dirac delta az egy olyan folytonos lineáris funkcionál ami minden tesztfüggvényhez (ez a korlátos tartójú végtelen sokszor differenciálható függvények osztálya) hozzárendeli a tesztfüggvénynek a 0-ban felvett értékét. És amit megadtál sorozat például ehhez tart. Ahogy még igen sok más sorozat is, ez nem a definíciója.
Most pedig térjünk rá a bizonyításodra is akkor:
"Legyen f(n) = delta(x-n) pi/2 + g(x) (1-delta(x-n))"
Ez badarság, a jobb oldal függ x-től, a bal oldal pedig nem. Gondolom arra gondoltál, hog
2011. július 23 00:39:44
Remélem nem utáltok ki innen, hogy most előveszek egy régebbi, meg nem válaszolt feladatot, és megolom:
Feladat (esernyo):
Folytasd a sorozatot (2)
1; 2; 6; 30; 210; ....
pi/2
Bizonyítás:
Köszönöm a bizalmat
Tehát a következő feladat: bizonyítsátok a Fermat tételt, lehetőleg 10-nél kevesebb oldalon.
Ki merészelné megtiltani? Akinek nem témája, az majd átugorja. Akinek tetszik, az meg olvassa, próbálja megérteni, és majd esetleg hasznosítani.
Én pl. simán látom magam előtt Ákos kollégám arcát, amint ezt előadom neki hétfőn reggel (hozzátéve, hogy mindezen tudást péntek /szombat éjjel szereztem ).
Várom az ítéleteteket: hány napig lesz megtiltva nekem az általános iskolai ötödik osztályosnál bonyolultabb matematikáról beszélni? :P
2011. július 23 00:37:51
Remélem nem utáltok ki innen, hogy most előveszek egy régebbi, meg nem válaszolt feladatot, és megolom:
Feladat (esernyo):
Folytasd a sorozatot (2)
1; 2; 6; 30; 210; ....
pi/2
Bizonyítás:
Megoldás: 6Kivontam a kecskéből a nem eheti meg a tavirózsát hegymászókötéllel. Innen triviális...
Hoppá, mi történt? Hiba? Írtam szöveget is, linkeltem képet is, illesztettem is be képet, mégis teljesen fehér és üres minden. Lát valaki valamit?
2011. július 23 00:36:18
Finom ez a banán hol vetted?
Tágabb értelemben.
Almádiba nővéremmel mentünk, aki Londonból jött haza... lehetséges-e, hogy én még nyugatabbról? :)
2011. július 22 23:58:22
Na akkor most egy olyan feladvány, amihez nem kell matekozni . Ez is régi, aki ismeri kérem a diszkréció fátyla fedje tudását.
Egy fiatal nő vesz egy kicsi panel lakást, és beköltözik egyedül. Éjszakánként viszont nem tud aludni, mert valami zavarja. Egy éjjel egy jó ötlete támad, fogja a telefonkönyvet, kikeres egy nevet, egy címet és persze a számot. Felhívja, és amikor a másik oldalon egy álmos férfihang szól a telefonba, ő szó nélkül leteszi. Ezután nyugodtan lefekszik, és elalszik.
Mi volt, ami zavarta?
Igen! Esernyő köszi a fátylat.
Megoldás: bizony bizony, a szomszéd horkolása zavarta éjjelente, és a telefonhívással ezt tudta megoldani. Megfejtő: GradU
2011. július 22 23:52:58
A megoldás a határértékszámításban kereshető: végtelen számú, nulla határértékű kifejezés összege nem feltétlenül nulla vagy végtelen, lehet egy véges, nullától kölönböző szám is.
Engem meggyőzött. Tetszik ez a bizonyítás.
A gond az, hogy úgy néz ki, mintha pi = 4 faktoriális lenne, pedig csak 4.
2011. július 22 23:22:14
Madarak
12 madár ül egy ágon, verebek és cinegék vegyesen. Az egyik fajból legalább fele annyi van, mint a másikból. Jön egy vadász, és lelövi azokat a páratlan sorszámú madarakat, melyek két szomszédja különböző fajta madár. Hány madár marad az ágon?
Esernyő: Valójában éppen Val-lal egy időben írtam a hozzászólást, nem az ő hozzászólására reagáltam ezt. De valóban jogos, hogy a mozgás is érzékelhető :).
gondold csak el, ha se nem látnak, se nem hallanak, akkor is érzik az ág mozgásából hogy valahogy kevesebb veréb vagy cinege ül rajta... :)
Mert ha látnak és hallanak, akkor elrepül az összes a lövés hangjára? Vagy már a puska puszta látványa elriasztja őket, mint a rutinos öreg kányát (na ez nem biztos, hogy kánya volt) a Tüskevárban?
Nem kötöttük ki, hogy milyen madarakról van szó, tehát mindkettőtök hozzászólását elfogadom megoldásként:
Megoldás: Egy madár sem marad az ágon, mert a túlélők mind elrepülnek a nagy lövöldözésre.
beküldők: esernyo, gradU
így van, ki kell kötni hogy süket, vak, és úgy mindenféle érzékeléssel nem rendelkező madarakról van-e szó :)
2011. július 22 23:03:19
Na inkább ide is leírom a véleményemet a megoldások külön jelöléséről, mert a "sűrűbe" írtam be. Vehetitek akár feladványnak is, aminek a megoldásán gondolkodunk. Bemásolom:
Igaza van a GradUnak, most, hogy már több feladvány fut egyszerre, a feladvány és a megoldás szétszóródna. Nagy lenne a kavarodás, talán már nem is szeretnénk az egészet. Tényleg vagy vastaggal kéne a megoldást írni, esetleg "Megoldás" címet adva neki, és csak a címet vastagon, vagy esetleg megvárnánk egymás feladványait, csak ez esetben működne a külön hozzászólásban írt megoldás. (Utóbbiban előfordulhat, ami a Szóláncban és a Képszámlálóban is, hogy nem tudjuk, a másik is írt valamit, és küldjük a miénket.)
Na úgy lesz jó! A vastagítással, és esetleg egy "megoldás" címmel egyértelmű lenne a társalgás listázásával
A gond az, hogy ha belelendülünk, akkor hamar eltűnik a megoldás a többi válasz fergetegében, melyek a megoldást tárgyalják, arról eszükbe jutó életérzésekről értekeznek, stb. De igazad van, főleg sok hozzászólás esetén még mindig jobb, mint teljesen külön hozzászólást nyitni. Ha valaki nagyon kíváncsi a megoldásra, kattintson a "társalgás listázása" gombra, és keresse meg.
Val drága? 
Ja, és a megfejtő nevét is oda írhatnánk, hamár külön, összesítve, külön írjuk a megoldást.
2011. július 22 22:45:55
Matematikai bizonyíték?
Vegyünk két számot, jelöljük őket mondjuk x-el és y-al.
Mi történik abban az estben, ha x = y ?
x = y
Megszorozzuk mindkét oldalt y-al:
x x = x y
x² = xy
kivonunk mindkét oldalból y² -et:
x² - y² = xy - y²
(x + y)(x - y) = y(x - y)
x + y = y
de mivel x = y,
x + x = x
vagyis éppen benizonyítottuk, hogy 2 = 1
Hogyan lehetséges? Mi a hiba a levezetésben?
2011. július 22 22:10:42
Folytasd a sorozatot (2)
1; 2; 6; 30; 210; ....
Megfejtő: Wapper
Megoldás: Az n. tagot úgy kapjuk meg, hogy az (n-1) tagot szorozzuk az prímszámok sorozatának (n-1). tagjával. A keresett tag a 2310. Az ilyen sorozatoknál általában van egy első tag, ez többnyire az egyes, az előre adott, de a 2. tag már kiszámolható, ezért nem jó az 1890-es megoldás.
Igen, pi = 3.1415926... amire gondoltam, vagy még hivatalosabban fogalmazva, a kör kerületének és átmérőjének arányára.
És szándékosa hibás matematikai bizonyítékokat sok félét lehet találni... hm, akkor egy ilyen lesz a következő feladat...
2011. július 22 22:09:30
Gimnáziumi logikai feladatmegoldó verseny feladatai... Az eredményekre már nem is emlékszem...
Folytasd a sorozatot (1)1; 2; 6; 15; 35; ...
A nulla az természetes szám. Egyszer matekversenyen láttam egy szegény szerencsétlen ötödikes körüli diákot vadul számolgatni a következő kérdés miatt: "mi az első ezer természetes szám szorzata". Szegény még százig sem jutott, és fel kellett adja...
Nem a feladat szempontjából volt fontos, hanem mert erről olyan jót beszélgettünk a minap matematikát kedvelő kollégámmal, és érdekelt a Ti véleményetek is.
Ha jól tudom az nem prímszám, mert csak 1 osztója van, míg a prímszámoknak meg kettő. De lehet hogy ez is olyan hogy most a 0 az természetes szám vagy nem.
